حساب حجم متوازي المستطيلات

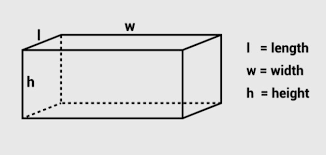
قانون حجم متوازي المستطيلات

متوازي المستطيلات هو شكل هندسي ثلاثي الأبعاد يتكون من ستة وجوه، حيث كل وجه هو مستطيل. يتميز متوازي المستطيلات بأن زواياه الداخلية قائمة (90 درجة)، وكل وجهين متقابلين لهما نفس الأبعاد. يُعد حساب حجم متوازي المستطيلات من الأمور الأساسية في الرياضيات والهندسة، وله تطبيقات عديدة في الحياة اليومية والمهنية. في هذه المقالة، سنستعرض كيفية حساب حجم متوازي المستطيلات مع تقديم أمثلة توضيحية.

تعريف متوازي المستطيلات

متوازي المستطيلات هو مجسم ثلاثي الأبعاد تكون جميع أوجهه على شكل مستطيلات. يتم تحديده بواسطة ثلاثة أبعاد رئيسية: الطول (L)، العرض (W)، والارتفاع (H).

حساب حجم متوازي المستطيلات

حجم متوازي المستطيلات هو مقدار الحيز الذي يشغله هذا المجسم في الفضاء. يُحسب حجم متوازي المستطيلات بضرب أبعاده الثلاثة معاً. يُعطى حجم متوازي المستطيلات بالعلاقة التالية:

$\text{حجم متوازي المستطيلات}=\text{الطول}\times \text{العرض}\times \text{الارتفاع}$

حيث:

• الطول (L) هو أحد أبعاد متوازي المستطيلات.
• العرض (W) هو البعد الثاني لمتوازي المستطيلات.
• الارتفاع (H) هو البعد الثالث لمتوازي المستطيلات.

مثال على حساب حجم متوازي المستطيلات

1. مثال بسيط: إذا كان لدينا متوازي مستطيلات أبعاده كالتالي: الطول = 5 سنتيمترات، العرض = 3 سنتيمترات، والارتفاع = 4 سنتيمترات، فإن حجمه يُحسب كالتالي: $\text{حجم متوازي المستطيلات}=5\times 3\times 4=60\text{ سنتيمتر مكعب}$
2. مثال آخر: إذا كان لدينا متوازي مستطيلات أبعاده كالتالي: الطول = 10 أمتار، العرض = 7 أمتار، والارتفاع = 2 متر، فإن حجمه يُحسب كالتالي: $\text{حجم متوازي المستطيلات}=10\times 7\times 2=140\text{ متر مكعب}$

أهمية حساب حجم متوازي المستطيلات

معرفة كيفية حساب حجم متوازي المستطيلات له أهمية كبيرة في العديد من التطبيقات الهندسية والعلمية واليومية. فهم هذه الحسابات يساعد في تصميم وتخطيط المساحات والأحجام، سواء في الهندسة المعمارية، التصميم الداخلي، أو حتى في التخزين والنقل.

تطبيقات عملية

1. الهندسة المعمارية والبناء:
   • يُستخدم حساب حجم متوازي المستطيلات في تصميم المباني والغرف.
   • تحديد كمية المواد المطلوبة للبناء، مثل الخرسانة والطوب.
2. التصميم الداخلي:
   • تصميم الأثاث وترتيب المساحات الداخلية يتطلب معرفة دقيقة لأحجام الأثاث والمساحات المتاحة.
3. التخزين والنقل:
   • يُستخدم حساب حجم متوازي المستطيلات في تخطيط وتوزيع البضائع في الحاويات والشاحنات.
4. الرياضة:
   • تُستخدم هذه الحسابات في تصميم أحجام الملاعب والمرافق الرياضية.
5. التعليم:
   • يُعتبر حساب حجم متوازي المستطيلات من المواضيع الأساسية في مناهج الرياضيات والفيزياء.

خلاصة

حساب حجم متوازي المستطيلات هو عملية بسيطة ومهمة في العديد من المجالات. يُحسب حجم متوازي المستطيلات بضرب أبعاده الثلاثة: الطول، العرض، والارتفاع. هذه العلاقة الرياضية الأساسية تجعل من السهل على الجميع فهم واستخدام هذه الحسابات في مجموعة متنوعة من التطبيقات اليومية والمهنية. فهم كيفية حساب حجم متوازي المستطيلات يساعد في تحقيق أفضل استغلال للمساحات المتاحة في مختلف المجالات الهندسية والعلمية.