دراسة المثلث متساوي الساقين

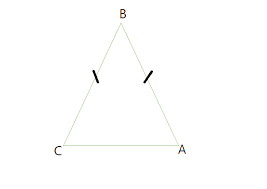
خصائص المثلث متساوي الساقين

المثلث متساوي الساقين هو نوع من أنواع المثلثات يتميز بأن له ضلعين متساويين في الطول، والضلع الثالث يختلف عنهما. يحتوي هذا المثلث على العديد من الخصائص الهندسية المهمة التي تجعله مميزًا. في هذه المقالة، سنستعرض خصائص المثلث متساوي الساقين مع تقديم بعض الأمثلة التوضيحية.

تعريف المثلث متساوي الساقين

المثلث متساوي الساقين هو مثلث له ضلعان متساويان في الطول، يُعرفان بالساقين، بينما يُعرف الضلع الثالث المختلف عنهما بالقاعدة. الزاويتان المتساويتان المجاورتان للقاعدة تُعرفان بالزاويتين القاعديتين.

خصائص المثلث متساوي الساقين

1. تساوي الزاويتين القاعديتين: في المثلث متساوي الساقين، الزاويتان القاعديتان المتجاورتان للقاعدة تكونان متساويتين في القياس. إذا كانت الزاوية عند الرأس تُعرف بـ $\theta$، فإن الزاويتين القاعديتين ستكونان 180∘−θ2\frac{180^\circ – \theta}{2}2180∘−θ​.
2. محور التماثل: يحتوي المثلث متساوي الساقين على محور تماثل يمر عبر الرأس وينصف القاعدة. هذا المحور يقسم المثلث إلى نصفين متطابقين.
3. الارتفاع من الرأس: الارتفاع المُسقط من الرأس على القاعدة يُنصف القاعدة، ويكون عموديًا عليها. هذا الارتفاع يقسم المثلث إلى مثلثين قائمين متطابقين.
4. تساوي الأضلاع المجاورة للقاعدة: الأضلاع المجاورة للقاعدة (الساقين) تكونان متساويتين في الطول.
5. القوانين الخاصة: يمكن استخدام بعض القوانين الرياضية الخاصة في المثلثات لحساب الأطوال والزوايا. على سبيل المثال، يمكن استخدام قانون فيثاغورس في المثلثات القائمة المتكونة عن تقسيم المثلث متساوي الساقين.

أمثلة توضيحية

1. مثال على الزوايا: إذا كان لدينا مثلث متساوي الساقين، وكانت الزاوية عند الرأس 40∘40^\circ40∘، فإن الزاويتين القاعديتين تُحسبان كالتالي: الزاوية القاعدية=180∘−40∘2=70∘\text{الزاوية القاعدية} = \frac{180^\circ – 40^\circ}{2} = 70^\circالزاوية القاعدية=2180∘−40∘​=70∘
2. مثال على الطول: إذا كان طول الساقين في مثلث متساوي الساقين 10 سم، وطول القاعدة 12 سم، يمكن حساب ارتفاع المثلث باستخدام نظرية فيثاغورس في أحد المثلثين القائمين المتكونين: h=102−62=100−36=64=8 سمh = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8 \text{ سم}h=102−62​=100−36​=64​=8 سم

أهمية دراسة المثلث متساوي الساقين

دراسة خصائص المثلث متساوي الساقين تساعد في حل العديد من المشاكل الهندسية والرياضية. فهم هذه الخصائص يمكن أن يكون مفيدًا في:

1. الهندسة المعمارية:
   • تصميم الهياكل المتماثلة مثل الأسقف والأبواب.
2. الفنون والتصميم:
   • استخدام الأشكال المتماثلة في الأعمال الفنية والتصميمات الجرافيكية.
3. التعليم:
   • توضيح المفاهيم الهندسية الأساسية للطلاب.

خلاصة

المثلث متساوي الساقين هو شكل هندسي بسيط ولكنه غني بالخصائص الهندسية المهمة. تساوي الزاويتين القاعديتين، ومحور التماثل، والارتفاع العمودي من الرأس هي بعض من هذه الخصائص التي تجعله مميزًا. فهم هذه الخصائص يساعد في تطبيقها في مجموعة متنوعة من المجالات الهندسية والفنية والتعليمية.