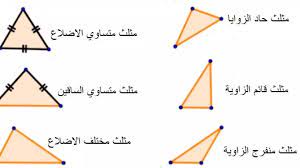
أهمية دراسة المثلث متساوي الأضلاع
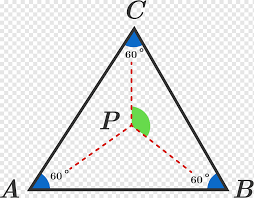
مثلث متساوي الأضلاع: تعريفه وخصائصه
المثلث متساوي الأضلاع هو أحد الأشكال الهندسية الأساسية في الرياضيات والهندسة، ويتميز بأن جميع أضلاعه متساوية في الطول وجميع زواياه متساوية في القياس. يعتبر هذا المثلث نموذجًا رائعًا للتناظر والتوازن الهندسي. في هذه المقالة، سنتناول تعريف المثلث متساوي الأضلاع، خصائصه، وكيفية حساب بعض الأبعاد المتعلقة به.
تعريف المثلث متساوي الأضلاع
المثلث متساوي الأضلاع هو مثلث تتساوى فيه جميع الأضلاع الثلاثة في الطول، وكذلك تتساوى جميع زواياه الداخلية. نظرًا لأن مجموع زوايا المثلث هو 180 درجة، فإن كل زاوية في المثلث متساوي الأضلاع تساوي 60 درجة.
خصائص المثلث متساوي الأضلاع
- تساوي الأضلاع: جميع أضلاع المثلث متساوي الأضلاع تكون متساوية في الطول. إذا كان طول أحد الأضلاع هو aa، فإن جميع الأضلاع الأخرى لها نفس الطول aa.
- تساوي الزوايا: جميع الزوايا الداخلية في المثلث متساوي الأضلاع تكون متساوية في القياس وتساوي 60 درجة.
- محور التماثل: المثلث متساوي الأضلاع يحتوي على ثلاثة محاور تماثل، كل منها يمر برأس من رؤوس المثلث وينصف الضلع المقابل له.
- الارتفاع: الارتفاع في المثلث متساوي الأضلاع يمكن حسابه باستخدام العلاقة التالية: h=32×ah = \frac{\sqrt{3}}{2} \times a حيث aa هو طول أحد الأضلاع.
- المساحة: مساحة المثلث متساوي الأضلاع يمكن حسابها باستخدام العلاقة التالية: المساحة=34×a2\text{المساحة} = \frac{\sqrt{3}}{4} \times a^2
- نصف القطر الدائري المحيط بالمثلث (R): نصف القطر الدائري المحيط بالمثلث متساوي الأضلاع يمكن حسابه باستخدام العلاقة التالية: R=a3R = \frac{a}{\sqrt{3}}
أمثلة توضيحية
- مثال على حساب الارتفاع: إذا كان طول الضلع في مثلث متساوي الأضلاع هو 6 سم، يمكن حساب الارتفاع كالتالي: h=32×6=33≈5.2 سمh = \frac{\sqrt{3}}{2} \times 6 = 3\sqrt{3} \approx 5.2 \text{ سم}
- مثال على حساب المساحة: إذا كان طول الضلع في مثلث متساوي الأضلاع هو 4 متر، يمكن حساب المساحة كالتالي: المساحة=34×42=34×16=43≈6.93 متر مربع\text{المساحة} = \frac{\sqrt{3}}{4} \times 4^2 = \frac{\sqrt{3}}{4} \times 16 = 4\sqrt{3} \approx 6.93 \text{ متر مربع}
أهمية دراسة المثلث متساوي الأضلاع
دراسة خصائص المثلث متساوي الأضلاع تعتبر مهمة في العديد من المجالات العلمية والهندسية. فهم هذه الخصائص يمكن أن يكون مفيدًا في:
- الهندسة المعمارية:
- تصميم الهياكل المتماثلة، مثل الأسقف والأبراج.
- تحسين الثبات والتوازن في الهياكل الهندسية.
- الفنون والتصميم:
- استخدام الأشكال المتناظرة في التصميمات الجرافيكية والفنون.
- تحقيق التوازن البصري في الأعمال الفنية.
- الرياضيات والتعليم:
- توضيح المفاهيم الهندسية الأساسية للطلاب.
- تعزيز الفهم العميق للتناظر والتوازن في الأشكال الهندسية.
خلاصة
المثلث متساوي الأضلاع هو شكل هندسي بسيط لكنه غني بالخصائص الهندسية المهمة. تساوي الأضلاع والزوايا، وجود محاور التماثل، وحساب الارتفاع والمساحة هي بعض من الخصائص التي تجعله مميزًا. فهم هذه الخصائص يساعد في تطبيقها في مجموعة متنوعة من المجالات الهندسية والفنية والتعليمية، مما يعزز القدرة على التصميم والإبداع والتحليل الهندسي.